Tasks

Define the problem, not the answer

The core feature of Multistep is its ability to evaluate substeps and give automated support. This is possible only if Multistep knows what problem students must solve. Therefore, you don't prescribe answers, but the tasks students should perform.

Example

a task could be to simplify $\frac{2y^2\sqrt{5}}{xy}$ . An answer is $2yx\sqrt{x}$ .
a task could be to solve $3(x-1)=2x+4$ . An answer is $x=7$ .

Algebrakit derives hints, error feedback, worked solutions, and answers from the task, so there is no need for you to input those. You can add custom hints or error feedback, as we will see later.

Multistep supports several tasks organized into the following categories:

Simplifying expressions
Performing numerical calculations, such as calculating percentages or converting units.
Rewriting expressions, such as expanding, factoring, or rewriting expressions into different forms.
Solving equations or inequalities
Calculus, such as differentiation, integration, or calculating limits.

You can build more complex tasks from these. For example:

Finding the equation of a line through two points, which requires:
1. Calculating the slope (Simplify).
2. Substitute coordinates to get the $y$ -intercept (Solve).
3. Writing the equation (Simplify).
Finding the coordinates of the maximum of a function, which requires:
1. Finding the derivative of the function (Differentiate)
2. Setting the derivative to zero and solving the equation (Solve)
3. Writing the coordinates of the maximum (Simplify)

How you create such composed tasks will be discussed in chapter Multistep (advanced)

Defining a task

Now let's create a new Multistep question. You can use the Testbench if you have no access to an Algebrakit-enabled content management system.

Selecting the Multistep question type Figure: Selecting the Multistep question type.

Click the icon for the Multistep question type to see the input form for Multistep. Click on the bar below 'Task' to expand it.

The input form for Multistep Figure: The input form for Multistep

The default Task is to simplify an expression. In the input field, type $x(x-1)+x$ .

Configuring a task Figure: Configuring a task

Now press the Test button at the bottom of the page to see a preview of our question.

Previewing an exercise Figure: Previewing our exercise.

The preview shows an interactive question on the left. You can answer the question step by step and request hints like a student would. The worked solution on the right shows how Algebrakit solves the problem. Click to expand the steps.

Note

See the table below if you are looking for information on the other input elements:

Task settings will be the topic of a following section
The Correct dropdown allows you to define custom student feedback.
The Hint toggle that allows you to add custom hints.
Preconditions will be described in the section Multistep (advanced).

The Simplify task

Simplifying is required with all tasks. Students must evaluate calculations and simplify expressions as much as possible.

$1+1$ must be evaluated to $2$
$x+y+x$ must be simplified to $2x+y$
$x(x+1)-x$ must be simplified to $x^2$

Multistep will only rewrite an expression if that simplifies the result. For example, Multistep will not rewrite the following expressions:

$x(x+1)$ . An equivalent form is $x^2+x$ .
Use the Expand task if you want the student to expand the expression.
$\frac{1}{x}+\frac{2}{3}$ . An equivalent form is $\frac{3+2x}{3x}$ .
Use the Combine Fractions task if you want the student to combine the fractions.

Multistep will accept such an equivalent form as a final answer.

Simplifying does not include solving equations, so Multistep will not require students to rewrite $2x=4$ into $x=\frac12$ . Use the Solve task if students should solve for $x$ .

Solving equations

In the category Solving Equations, you can find tasks for finding solutions to equations, inequalities, or systems of two equations.

Task: Solving Equations Figure: Task: Solving Equations

You can use the "Solving Equations: Single Variable" task to solve a wide variety of relations. The table shows some examples:

Relation	Result	Explanation
$6(p-1)=4p+10$	$p=8$	A linear equation
$a\cdot x=b$	$x=\frac{b}{a}$	Algebraic solutions are allowed
$2(1-x)\leq4$	$x\geq -1$	Inequalities are supported
$\frac{1}{\sqrt{1-x}}>1$	$0<x<1$	Algebrakit keeps track of the domain
$2\sin \left(2x-\frac{1}{4}\pi \right)=\sqrt{2}$ , $0<x<\pi$	$x=\frac{\pi}{4}, x=\frac{\pi}{2}$	Trigonometry
$\begin{cases}2x-1=y\\x+y=1\end{cases}$	$\begin{cases}x=\frac{2}{3}\\y=\frac{1}{3}\end{cases}$	System of two equations

As always, Multistep offers support through hints and substep evaluations. You can try them here:

Note

The following type of equations are not yet supported

Systems of more than two equations
Systems of inequalities
Equations with solutions in the complex plane

Other tasks

We invite you to check out the other tasks in the Multistep editor. Most of them will be self-explanatory. The table below shows some examples.

Task	Example	Result
Expand	$x(x-1)$	$x^2-x$
Factor	$x^2-x$	$x(x-1)$
Combine Fractions	$\frac{1}{x}+\frac{2}{3}$	$\frac{3+2x}{3x}$
Complete the Square	$x^2+6x+7$	$\left(x+3\right)^2-2$
Differentiate	$\sin\left(2x^2\right)$	$4x\cos\left(2x^2\right)$
Integrate	$4x\cos\left(2x^2\right)$	$\sin\left(2x^2\right) + c$

Initial expression

Multistep default starts with an empty work area. You can use the dropdown "Initial expression" to make the first expression of the derivation visible to students. This first expression is generally the expression you gave in the task but you can also define a custom expression.

A Multistep with and without an initial expression Figure: A Multistep with and without an initial expression.

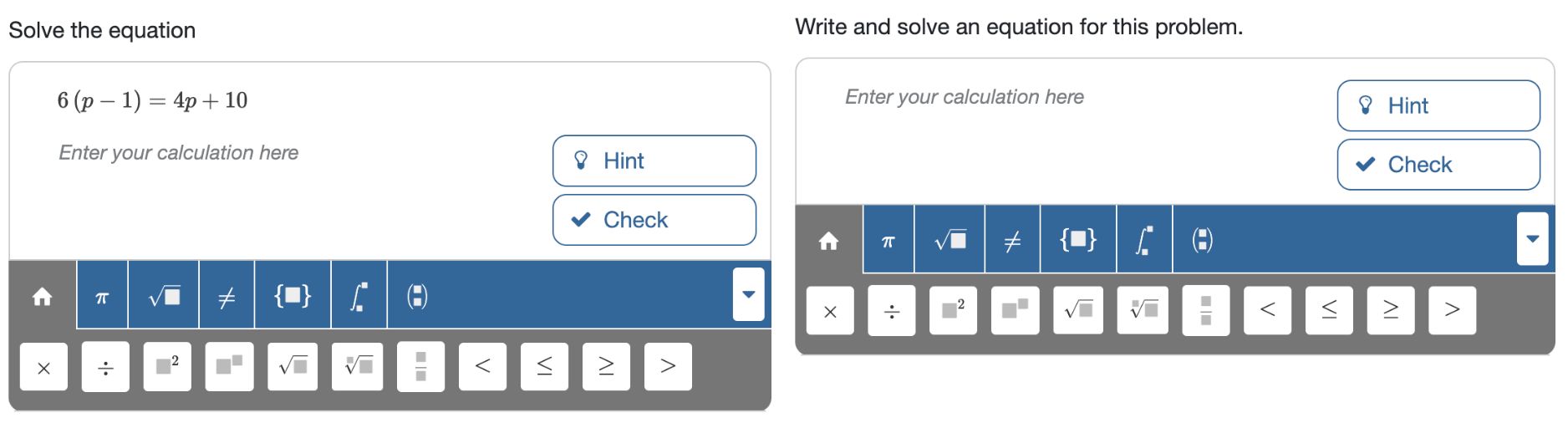
Custom feedback

Although Multistep can show error feedback for some common mistakes, you sometimes want to add custom error feedback. You can achieve this by adding an incorrect task.

Hover your mouse over the taskbar and use the Add button to add the new task.

Add feedback Figure: Adding a task. Hover your mouse over the task to see these task buttons

Use the dropdown in the new task to indicate that this activity is incorrect. You can add custom error feedback as well.

Custom feedback Figure: Specifying custom feedback in an "incorrect" task

Algebrakit will show the feedback when a student inputs an expression that matches this task.

Custom feedback

Custom hints

Algebrakit can automatically generate hints from the task. Sometimes you want to add custom hints and feedback.

Initial hints

You can define hints that Algebrakit must show before the automatic hints. For example, you can add custom hints to help students getting started by rephrasing the question.

When you create a Multistep exercise, click on Multistep and choose Hints. Adding a custom initial hint Figure: Adding a custom initial hint

You can add multiple hints using the plus icon on the right. Adding multiple custom hints Figure: Adding multiple custom hints

Custom hints on task level

You can also add your custom hints to tasks. Algebrakit will show these custom hints before any generated hints about that specific task.

Adding a custom hint to a task Figure: Adding a custom hint to a task

Custom hints showing in the Multistep question Figure: Two hints in the Multistep question. Algebrakit shows the custom hint before the generated hint.

Disabling automated hints

Students can request multiple hints by repeatedly clicking the Hint button. The hints will appear in the following order:

The custom initial hint(s)
The custom hint(s) defined in the task, combined with the task description (if defined)
The automated hint(s) from the task

To disable automated hints, click on Multistep and choose Settings.

Disabling automated hints Figure: Disabling automated hints

Configuring hints in the settings panel Figure: Configuring hints in the settings panel

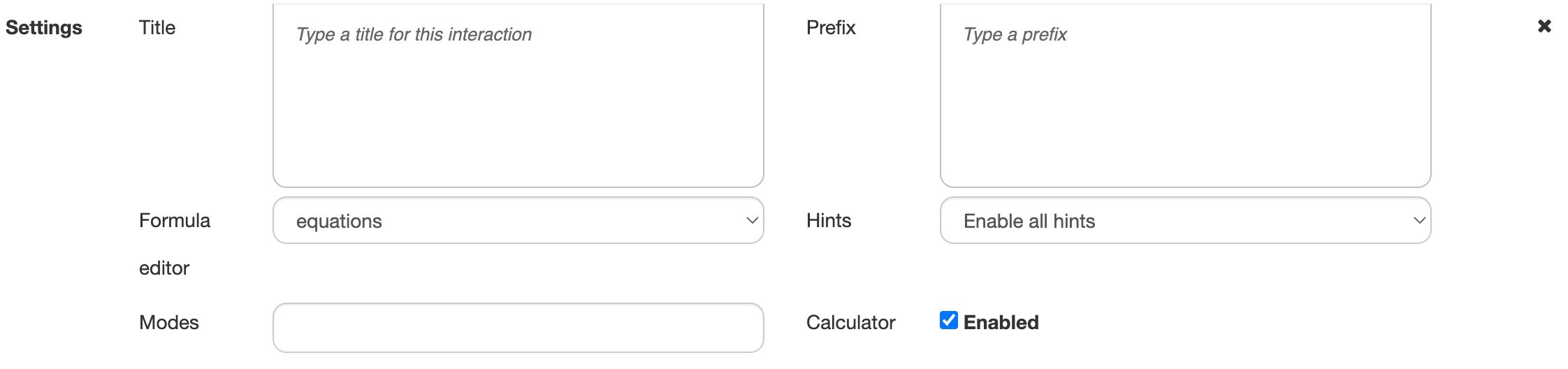
The Hints dropdown offers the following options:

Enable all hints: Enable custom hints and Algebrakit's automated hints.
Disable automated hints, but generate hints based on descriptions: Custom initial hints and task hints will be shown. In case of multi-part questions, hints from the task description will be shown. No automated hints of mathematical steps will be shown.
Disable automated hints: Custom initial hints and task hints will be shown. No automated hints of Algebrakit will be shown