Multi-part algebra

From arithmetic to algebra

In the previous section, you saw how to define a solution model for multi-part arithmetic exercises. We will now extend this to questions that involve algebra. The difference between algebra and arithmetic questions is that the solution uses variables and equations. Here are two examples of multi-part problems that involve algebra:

"Find the formula of the linear line intersecting $(1,3)$ and $(3,-1)$ ."
"A rectangular piece of land has an area of $2400 m^2$ . The length of the land is $20 m$ longer than the width. What is the total length $L$ of a fence surrounding this land?"

We will create both examples using the Multistep question type. You can try them in the live examples below:

Live example: The multi-part algebra problems.

Example 1: The formula of a line

Consider the first example.

Example problem 1

Find the formula $y=mx+b$ for the line intersecting $(1,3)$ and $(3,-1)$ .

The solution to this problem requires the following parts:

Calculate the slope, $m$
Find the $y$ -offset, $b$ , by substituting one of the given points
Write the formula for $y$ .

We turn this into a solution model as follows:

Part	Description	Calculation	Marks
$y$	the requested formula	$y=m\cdot x+b$	1
$m$	the slope	$\frac{-1-3}{3-1}$	1
$b$	the $y$ -intercept	Solve $3=m\cdot 1+b$ for $b$	1

Note

Note that we did not define the part for $y$ as $y=5-2x$ , which is the answer to the problem. Instead, we keep variables $m$ and $b$ to let Algebrakit know these are required to find the solution. You can also see that the slope $m$ is needed to calculate the $y$ -offset. Algebrakit will calculate the slope first, followed by the $y$ -intercept, and the solution.

Now let's create this question in Multistep.

Add two new exercise parts and name them $m$ and $b$ .
Add the descriptions to the parts as given in the solution model.
Set the tasks corresponding to the calculations in the solution model. Choose task Solve equations for exercise part $m$ and Simplify for the other exercise parts.
In the menu of the part names $y$ , $m$ and $b$ , check the option student variable as shown in the screenshot below.

Enabling student variables Figure: Enabling student variables.

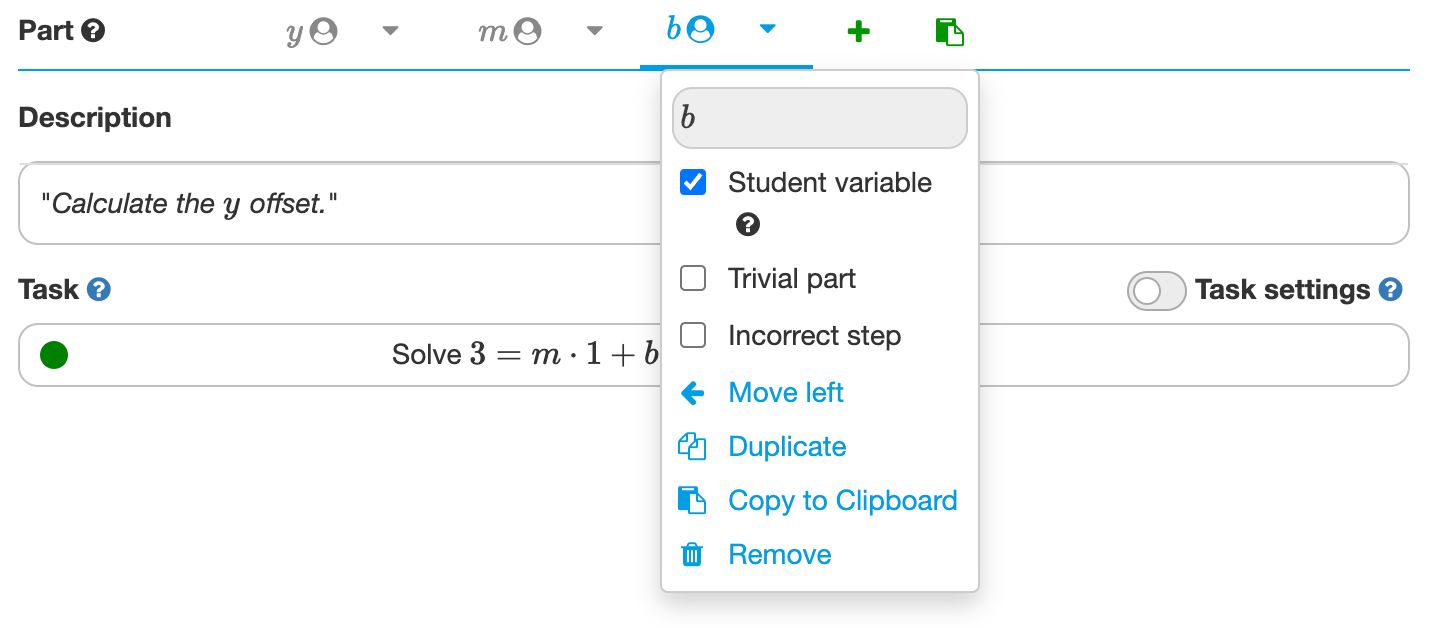
Student variables

An important step is checking option Student variable in the exercise parts $y$ , $m$ and $b$ . Names of exercise parts are just references to other parts and are not visible to students. However, when you configure a part name as a student variable, it becomes a variable students can use in their work.

If you do not configure $m$ and $b$ as student variables, Algebrakit will not correctly interpret expressions that involve these variables. Here are some examples.

Student input	Evaluation with student variables	Evaluation without student variables
$y=mx+b$	Correct intermediate step. Algebrakit understands $m$ and $b$ still need to be calculated.	Incorrect. Algebrakit does not allow using $m$ or $b$ .
$-2$	Correct intermediate step. The input is assumed to correspond to the slope.	Same
$m=-2$	Correct intermediate step. Algebrakit understands that $m$ is the slope, which equals -2.	Incorrect. Algebrakit does not interpret $m$ as the slope.
$m\cdot 3+b=-1$	Correct intermediate step. Algebrakit knows that $m=-2$ and $b=5$ , so the relation is valid.	Incorrect. Algebrakit does not allow using $m$ or $b$ .

This is a significant improvement. Students can now build their solutions by writing formulas and equations first and solving them later. From a didactical point of view, we transitioned from arithmetic to algebraic thinking.

Example 2: An algebra word problem

We will now create the second example question:

Example problem 2

A rectangular piece of land has an area of $2400 m^2$ . The length of the land is $20 m$ longer than the width.

What is the total length $L$ of a fence that surrounds this land?

You can solve this problem in two ways:

Calculating the width first:
- Find the width $w$ by solving equation $w(w+20)=2400$
- Find the circumference as $2w+2(w+20)$ .
Calculating the length first:
- Find the height $l$ by solving equation $l(l-20)=2400$
- Find the circumference as $2l+2(l-20)$ .

Which results in the following solution models:

Part	Description	Calculation	Marks
$w$	the width of the land	Solve $w(w+20)=2400$	1
$L$	the length of the fence	$2w+2(w+20)$	1

Part	Description	Calculation	Marks
$l$	the length of the land	Solve $l(l-20)=2400$	1
$L$	the length of the fence	$2l+2(l-20)$	1

You add these to Multistep as follows:

Add two new exercise parts with names $w$ and $l$ . Rename the solution part to $L$ .
Check the Student variable option on all three exercise parts.
Add the descriptions to all exercise parts
Set the tasks. Use the Simplify task for $L$ and the Solve equations task for $w$ and $l$ .

If you test the exercise, you will see that Algebrakit complains about student variable $w$ .

Error message when a student variables does not have a single value

The issue is that the equation $w(w+20)=2400$ has two solutions: $w=-60$ and $w=40$ . To not complicate things, Algebrakit only allows using $w$ as a student variable if it has a single result. You can solve this problem by adding the domain $w>0$ to the equation, as shown below:

Adding a domain to enforce a single result Figure: Adding a domain to enforce a single result.

Add a domain to exercise part $l$ as well. You should now be able to run the question.

Free variables

The exercise already works well. You can apply algebraic thinking, using formulas and equations for variables $L$ , $w$ , and $l$ , and Algebrakit will understand. But we can go even further.

The instruction does not mention variables $w$ and $l$ . Even more, the question does not indicate that you should variables at all. It is apparently up to the student to come up with that approach. This is an example of modelling, an important mathematical skill.

So now we have the problem that the solution model assumes students use variables $w$ or $l$ , but we don't want to include that information in the instruction. The solution is to declare $w$ and $l$ as free variables. This means that students do not have to use the same variable name but are free to choose.

You declare a free variable in the symbols tab on the top bar.

Defining free variables Figure: Defining free variables.

The example below shows an example of a correct solution to this problem.

Choosing custom variable names when solving the question Figure: Choosing custom variable names when solving the question.

Note

A free variable must be a single symbol. So students cannot use a variable name like ' $width$ '.

Restrictions when using student variables

These examples show how student variables are a powerful concept that helps students to apply algebraic thinking. However, there are a few limitations when using this technique.

Student variables must have exactly one solution. We saw this already in the second example. If the variable is defined by an equation, you might have to add a domain. Note that it is also not ok if the equation has no solutions.
Student variables cannot refer to each other. Assume $a$ and $b$ are student variables. If the task for $a$ depends on $b$ and the task for $b$ depends on $a$ , then Algebrakit will show an error message if you try to run the exercise. The reason is that no order exists to calculate the results for each part. This is currently not supported.