Multi-part calculus

Introducing functions in multi-part exercises

We introduced variables to support algebraic reasoning in multi-part exercises. We will now extend this concept to support calculus, which is about the analysis of functions.

Here are two examples of such multi-part calculus questions.

Finding the formula of the tangent to a given function
Finding the dimension of a box with maximum volume

We will discuss both examples below.

Example: Formula for the tangent

Consider the following example.

Find the formula of the tangent to $f(x)=2x^2-x$ at coordinates $(2,6)$ .

The solution to this problem requires the following parts:

Deriving the derivative function $f'(x)$ .
Calculating the slope of the tangent $m = f'(2)$ .
Finding the $y$ -offset, $b$ , by substituting $(x,y)=(2,6)$ .
Writing the requested formula $y=mx+b$ .

We turn this into a solution model as follows:

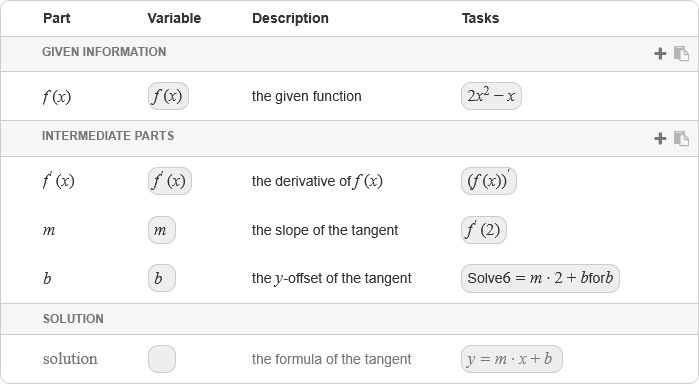
Part	Description	Calculation	Marks
$f'(x)$	the derivative of $f(x)$	The derivative of $x^2-x$ for $x$	1
$m$	the slope	$m=f'(2)$	1
$b$	the $y$ -offset	Solve $6=m\cdot 2+b$ for $b$	1
solution	the formula of the tangent	$y=m\cdot x+b$	1

Now, let's create this question in Multistep.

Add three new exercise parts and name them $f'(x)$ , $m$ and $b$ .
Add the corresponding variable to each part.
Set the descriptions of the exercise parts as in the above table.
Set the tasks corresponding to the calculations in the solution model. Choose Solving equations/Single variable for $b$ and Simplify for $m$ . For exercise part $f'(x)$ , choose Simplify and set the task as $(f(x))'$ .

Overview of a calculus problem. Figure: Overview of a calculus problem.

Here is a live example of the problem we just created:

Live example: The multi-part calculus problem.

Function definition as exercise part

This example shows that exercise parts can also define functions and their derivatives. Set the name of the part's variable to the function, including the variable arguments. Do not repeat the function name in the task.

Example

To define function $T(t)=2\sqrt{1+t}$ :

Create a part
Set the part's variable to $T(t)$
Define the part's task as Simplify $2\sqrt{1+t}$ .

You can define derivatives in the same way, using a variable name such as $f'(x)$ or $\frac{df}{dx}(x)$ .

A variable name like $f'(x)$ is more than just a name. Algebrakit interprets this as a function definition. To see how powerful this is, consider the following optional student inputs:

Student input	Evaluation
$y=f'(2) x+b$	Correct intermediate step. Algebrakit understands that $f'(2)=7$ and $b=-8$ .
$f(0)=0$	Correct expression, which follows from the definition $f(x)=x^2-x$ .
$m=f'(2)$	Correct intermediate step to calculate the slope $m$ .

Example: A calculus word problem

Let's now create the following word problem:

Folding a box out of a square cardboard You can create a box from a square piece of cardboard by cutting a square from each corner and folding the sides. If the dimensions of the cardboard are $30 m\times 30cm$ , calculate the value of $h$ that maximizes the volume $V(h)$ of the box.

The solution to this problem requires the following parts:

Writing an expression for the width of the box $w=30-2h$ ,
Writing a formula for the volume $V(h)=h\cdot w\cdot w = h(30-2h)^2$ ,
Deriving the derivative $V'(h)$ ,
Solving $V'(h)=0$ , with $0\lt h \lt 15$ .

We turn this into a solution model as follows:

Part	Description	Calculation	Marks
$w$	an expression for the width $w$ of the box	$30-2h$	1
$V(h)$	the volume of the box	$h\cdot w^2$	1
$V'(h)$	the derivative of the volume w.r.t. $h$	$\frac{d}{dh} V(h)$	1
solution	the height $h$ of the box width maximum volume	Solve $V(h)=0$ with domain $0\lt h \lt 15$	1

You can find a live example of the problem below. Click the Edit button to see how we made this exercise.

Live example: Finding the dimensions of a box with maximum volume.