Evaluation Criteria

We have seen how tasks allow Algebrakit to handle many things automatically. However, sometimes you want to influence how Algebrakit behaves. In that case you can add custom criteria to evaluate student input.

Use cases of evaluation criteria

There are several situations that require the use of evaluation criteria.

• To accept additional final answers.
  • Nonsimplified input
    Let students write a calculation, like "$3\times 1.25$", without evaluating it. Remember that tasks will always force students to simplify their answers.
  • Alternative notations
    For example, the solution of an equation is $x=42$ and you want to accept input $42$ as well.
  • Non-math notations
    The answer of the question is not a mathematical expression. An example is time notation, like “15:04”.
• To add custom error feedback
  For example, the solution of an equation is $x=42$ and you want to provide feedback if the student answers $42$.
• For open questions that have multiple correct answers
  The answer of the question can be any expression that matches some condition. For example, "write a divisor of 36".

The elements of evaluation criteria

Figure: A criterium to give error feedback when students input an expression that is equivalent to $2t-t^2$.

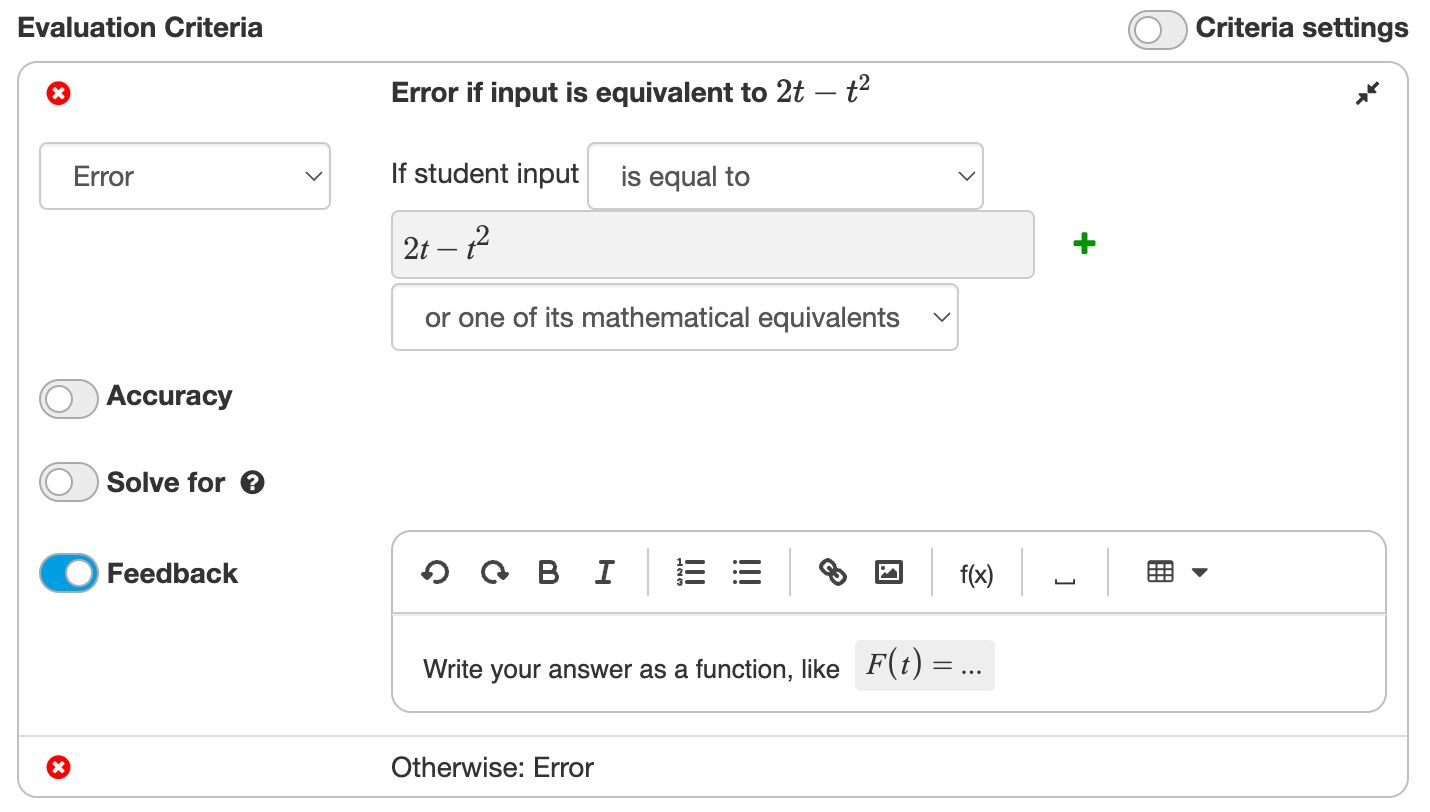
An evaluation criterium contains the following parts:

• The condition determines to what student input the criterium applies. This can be an equality condition or a logical expression.
• The result indicates what happens if the condition is met. There are three options:
  • Finish: the student input is a correct final answer
  • Intermediate step: the student input is correct but needs simplification
  • Error: the student input is not correct
  • Unknown: the student input could be correct or incorrect.
• Feedback. You can optionally provide feedback to students when the criterium matches. This usually applies when the student input is not correct.

Equality conditions

Figure: An equality criterium.

An equality criterium applies if the students input is equal to one of the given expressions. There are different types of equality:

• Mathematically equivalent applies to solutions of relations.
  Example: $2x=4$ is equal to $x=2$ because they have the same solution.
• Mathematically equal applies to equivalent expressions, without solving relations. Example: $y=x(x+1)$ is equal to $y=x^2+x$, but not to $x^2+x-y=0$.
• Equal up to commutativity applies to the order of commutative operators, such as $+$, $\times$, and $=$.
  Example: $2x+4$ is equal to $4+x\cdot 2$, but $x+x$ is not equal to $2x$.
• Textually equal means that the expression must be visually identical. Only spaces are neglected.
  Algebrakit will not attempt to interpret the expression. This allows you to use nonmathematical expressions.
  Example: $x+4$ is not equal to $4+x$.

Boolean conditions

Figure: A criterium with a boolean condition.

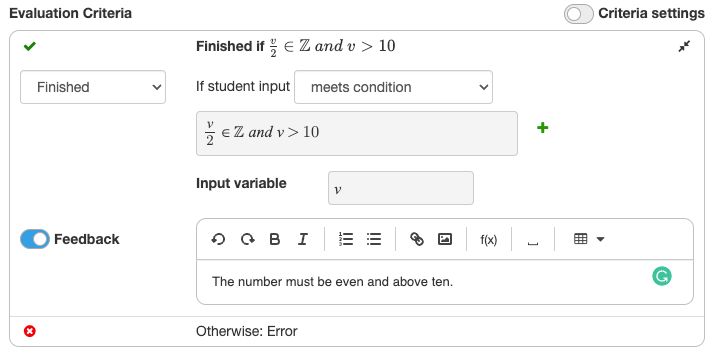
Evaluation criteria also allow you to create questions that have more than one answer, such as:

• "Write a positive integer value"
• "Write an even number"
• "Write a value of $x$, such that $\sin(3\pi x)=0$."

In such cases, you create an evaluation criterium that checks for a boolean condition, using a variable that represents the student's input.

Boolean conditions are also useful for tables. For example, you can let students create a function table without prescribing the function values. You will see examples when we discuss the Math Table question type.

Multiple evaluation criteria

Figure: Using multiple criteria.

You can use multiple criteria to build complex evaluation rules. Algebrakit will evaluate the criteria from top to bottom and use the first criterium that matches.